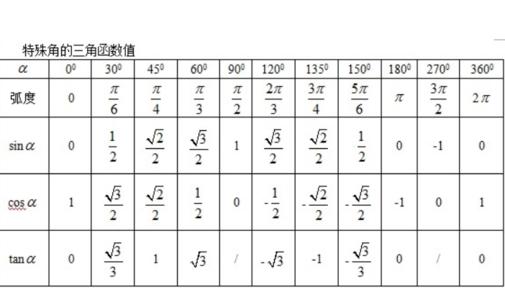
三角函数导数公式大全
的有关信息介绍如下:
倒数关系: tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 商的关系: sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα 平方关系: sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式 sin^2(α)+cos^2(α)=1 tan α *cot α=1一个特殊公式 (sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ) 证明:(sina+sinθ)*(sina-sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin(a+θ)*sin(a-θ)坡度公式 我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比), 用字母i表示, 即 i=h / l, 坡度的一般形式写成 l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作 a(叫做坡角),那么 i=h/l=tan a.锐角三角函数公式 正弦: sin α=∠α的对边/∠α 的斜边 余弦:cos α=∠α的邻边/∠α的斜边 正切:tan α=∠α的对边/∠α的邻边 余切:cot α=∠α的邻边/∠α的对边二倍角公式 正弦 sin2A=2sinA·cosA 余弦 1.Cos2a=Cos^2(a)-Sin^2(a) 2.Cos2a=1-2Sin^2(a) 3.Cos2a=2Cos^2(a)-1 即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a) 正切 tan2A=(2tanA)/(1-tan^2(A))三倍角公式 sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a = tan a · tan(π/3+a)· tan(π/3-a) 三倍角公式推导 sin(3a) =sin(a+2a) =sin2acosa+cos2asina =2sina(1-sin²a)+(1-2sin²a)sina =3sina-4sin^3a cos3a =cos(2a+a) =cos2acosa-sin2asina =(2cos²a-1)cosa-2(1-cos^a)cosa =4cos^3a-3cosa sin3a=3sina-4sin^3a =4sina(3/4-sin²a) =4sina[(√3/2)²-sin²a] =4sina(sin²60°-sin²a) =4sina(sin60°+sina)(sin60°-sina) =4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a) cos3a=4cos^3a-3cosa =4cosa(cos²a-3/4) =4cosa[cos²a-(√3/2)^2] =4cosa(cos²a-cos²30°) =4cosa(cosa+cos30°)(cosa-cos30°) =4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°) =-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)] =-4cosacos(60°-a)[-cos(60°+a)] =4cosacos(60°-a)cos(60°+a) 上述两式相比可得 tan3a=tanatan(60°-a)tan(60°+a) 现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α)) cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。包括一些图像问题和函数问题中三倍角公式 sin3α=3sinα-4sin^3(α)=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cos^3(α)-3cosα=4cosα·cos(π/3+α)cos(π/3-α) tan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)=tan a · tan(π/3+a)· tan(π/3-a)半角公式 sin^2(α/2)=(1-cosα)/2 cos^2(α/2)=(1+cosα)/2 tan^2(α/2)=(1-cosα)/(1+cosα) tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα万能公式 sinα=2tan(α/2)/[1+tan^2(α/2)] cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] tanα=2tan(α/2)/[1-tan^2(α/2)]其他 sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0 cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及 sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2 tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式 sin4A=-4*(cosA*sinA*(2*sinA^2-1)) cos4A=1+(-8*cosA^2+8*cosA^4) tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式 sin5A=16sinA^5-20sinA^3+5sinA cos5A=16cosA^5-20cosA^3+5cosA tan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式 sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2)) cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1)) tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式 sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6)) cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7)) tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式 sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1)) cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2) tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式 sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3)) cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3)) tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)十倍角公式 sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^4)) cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1)) tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)N倍角公式 根据棣美弗定理,(cosθ+ i sinθ)^n = cos(nθ)+ i sin(nθ) 为方便描述,令sinθ=s,cosθ=c 考虑n为正整数的情形: cos(nθ)+ i sin(nθ) = (c+ i s)^n = C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n-4)*(i s)^4 + ... +C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... =>比较两边的实部与虚部 实部:cos(nθ)=C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n-4)*(i s)^4 + ... i*(虚部):i*sin(nθ)=C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... 对所有的自然数n, 1. cos(nθ): 公式中出现的s都是偶次方,而s^2=1-c^2(平方关系),因此全部都可以改成以c(也就是cosθ)表示。 2. sin(nθ): (1)当n是奇数时: 公式中出现的c都是偶次方,而c^2=1-s^2(平方关系),因此全部都可以改成以s(也就是sinθ)表示。 (2)当n是偶数时: 公式中出现的c都是奇次方,而c^2=1-s^2(平方关系),因此即使再怎么换成s,都至少会剩c(也就是 cosθ)的一次方无法消掉。 (例. c^3=c*c^2=c*(1-s^2),c^5=c*(c^2)^2=c*(1-s^2)^2)半角公式 tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA. sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a)) 和差化积 sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2] sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2] cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2] cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2] tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)两角和公式 tan(α+β)=(tanα+tanβ)/(1-tanαtanβ) tan(α-β)=(tanα-tanβ)/(1+tanαtanβ) cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ sin(α+β)=sinαcosβ+cosαsinβ sin(α-β)=sinαcosβ -cosαsinβ积化和差 sinαsinβ =-[cos(α+β)-cos(α-β)] /2 cosαcosβ = [cos(α+β)+cos(α-β)]/2 sinαcosβ = [sin(α+β)+sin(α-β)]/2 cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数 sh a = [e^a-e^(-a)]/2 ch a = [e^a+e^(-a)]/2 th a = sin h(a)/cos h(a) 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)= sinα cos(2kπ+α)= cosα tan(2kπ+α)= tanα cot(2kπ+α)= cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin(π+α)= -sinα cos(π+α)= -cosα tan(π+α)= tanα cot(π+α)= cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)= -sinα cos(-α)= cosα tan(-α)= -tanα cot(-α)= -cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)= sinα cos(π-α)= -cosα tan(π-α)= -tanα cot(π-α)= -cotα 公式五: 利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)= -sinα cos(2π-α)= cosα tan(2π-α)= -tanα cot(2π-α)= -cotα 公式六: π/2±α及3π/2±α与α的三角函数值之间的关系: sin(π/2+α)= cosα cos(π/2+α)= -sinα tan(π/2+α)= -cotα cot(π/2+α)= -tanα sin(π/2-α)= cosα cos(π/2-α)= sinα tan(π/2-α)= cotα cot(π/2-α)= tanα sin(3π/2+α)= -cosα cos(3π/2+α)= sinα tan(3π/2+α)= -cotα cot(3π/2+α)= -tanα sin(3π/2-α)= -cosα cos(3π/2-α)= -sinα tan(3π/2-α)= cotα cot(3π/2-α)= tanα (以上k∈Z) A·sin(ωt+θ)+ B·sin(ωt+φ) = √{(A² +B² +2ABcos(θ-φ)} · sin{ ωt + arcsin[ (A·sinθ+B·sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表示根号,包括{……}中的内容三角函数的诱导公式(六公式) 公式一 sin(-α) = -sinα cos(-α) = cosα tan (-α)=-tanα 公式二sin(π/2-α) = cosα cos(π/2-α) = sinα 公式三 sin(π/2+α) = cosα cos(π/2+α) = -sinα 公式四sin(π-α) = sinα cos(π-α) = -cosα 公式五sin(π+α) = -sinα cos(π+α) = -cosα 公式六tanA= sinA/cosA tan(π/2+α)=-cotα tan(π/2-α)=cotα tan(π-α)=-tanα tan(π+α)=tanα 诱导公式记背诀窍:奇变偶不变,符号看象限万能公式 sinα=2tan(α/2)/[1+(tan(α/2))²] cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²] tanα=2tan(α/2)/[1-(tan(α/2))²] 其它公式 (1) (sinα)^2+(cosα)^2=1(平方和公式) (2)1+(tanα)^2=(secα)^2 (3)1+(cotα)^2=(cscα)^2 证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可 (4)对于任意非直角三角形,总有 tanA+tanB+tanC=tanAtanBtanC 证: A+B=π-C tan(A+B)=tan(π-C) (tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC) 整理可得 tanA+tanB+tanC=tanAtanBtanC 得证 同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立 由tanA+tanB+tanC=tanAtanBtanC可得出以下结论 (5)cotAcotB+cotAcotC+cotBcotC=1 (6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2) (7)(cosA)^2;+(cosB)^2+(cosC)^2=1-2cosAcosBcosC (8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC 其他非重点三角函数 csc(a) = 1/sin(a) sec(a) = 1/cos(a) (seca)^2+(csca)^2=(seca)^2(csca)^2 幂级数展开式 sin x = x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。 (-∞