darboux定理是什么？

darboux定理是什么？

darboux定理是达布中值定理。设y=f(x)在(A,B)区间中可导，且[a,b]包含于(A,B)，f'(a)<f'(b)，则对于任意给定的η:f'(a)<η<f'(b),都存在一点c∈(a,b)使得f'(c)=η。

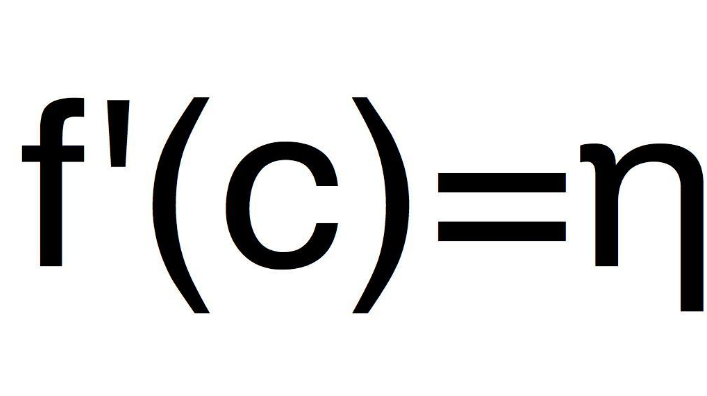
darboux定理证明：

方法1：

已知f'(a)<η<f'(b)，构造函数：g(x)=f(x)-ηx。

若g(a)=g(b)，则由罗尔中值定理：存在ε∈(a,b)使g'(ε)=0。

不妨设g(a)>g(b)，又g'(b)>0，由极限保号性，存在ξ∈（a,b）使g(ξ)<g(b)<g(a)。

由介值定理存在ζ∈(a,ξ)使g(ζ)=g(b)。

又由罗尔中值定理，存在δ∈(ζ,b)使g'(δ)=0。

所以无论如何总存在x∈(a,b)使g'(x)=0即f'(x)=η。

方法2：

构造函数g(x)=f(x)-ηx。

由于f(x)在(a,b)区间内可导，所以f(x)在(a,b)区间内连续，故g(x)在(a,b)区间内连续。

补充定义使得g(x)在x=a，x=b处连续。

因为g'(a)=f'(a)-η<0,所以一定存在x>a,使得g(x)<g(a)。

即x=a不是函数g(x)在[a,b]上的最小值，同理x=b也不是函数g(x)在[a,b]上的最小值。

故g(x)在(a,b)区间内取得最小值。

所以必然存在ξ∈(a,b)，使g'(ξ)=f'(ξ)-η=0（费马定理）。

所以对于任意给定的η:f'(a)<η<f'(b),都存在一点c∈(a,b)使得f'(c)=η。