如何理解导函数中间值定理(又名达布中值定理)?

如何理解导函数中间值定理(又名达布中值定理)?

理解导函数中间值定理(又名达布中值定理)：不可以直接用，要真的考到只有在大题里分布设问题，先叫你证明这个，再用这个定理证明其他结论，在选择填空里知道的结论都能用。

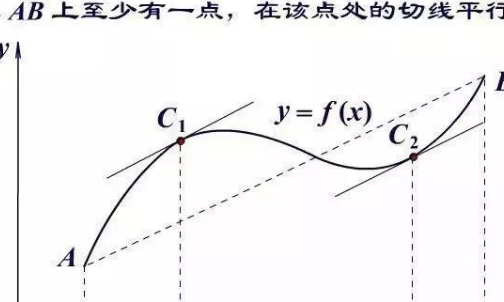
做辅助函数g（x）=f（x）-rx

在［a，b］连续，由闭区间连续函数存在最大最小值

则存在c∈［a，b］有g（c）是最值

由费马定理g'（c）=0

即f'（c）=r

含义

若将一点扩展成函数f(x)在其定义域包含的某开区间I内每一个点，那么函数f(x)在开区间内可导，这时对于内每一个确定的值，都对应着f(x)的一个确定的导数，如此一来每一个导数就构成了一个新的函数，这个函数称作原函数f(x)的导函数，记作：y'或者f′(x)。