基本不等式有哪三种？

基本不等式有哪三种？

基本不等式有两种：基本不等式和推广的基本不等式（均值不等式）

基本不等式是主要应用于求某些函数的最大（小）值及证明的不等式。其表述为：两个正实数的算术平均数大于或等于它们的几何平均数。

（1）基本不等式

两个正实数的算术平均数大于或等于它们的几何平均数。

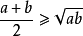
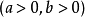
（2）推广的基本不等式（均值不等式）

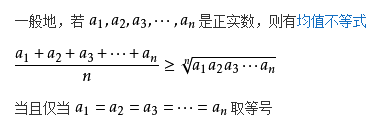
时不等式两边相等。

不等式运用示例

某学校为了美化校园,要建造一个底面为正方形,体积为32的柱形露天喷水池,问怎样才能使得用来砌喷水池底部和四壁的镶面材料花费最少?

答：设底面正方形边长为x，则水池高为32/x^2

y=x^2+4x*32/x^2=x^2+128/x=x^2+64/x+64/x

≥3(1*64*64)^(1/3)=48

所以当x^2=64/x,x=4时花费最少。 

上面解法使用了均值不等式

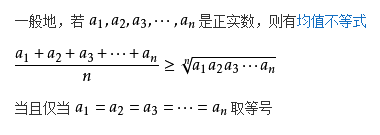
时不等式两边相等。