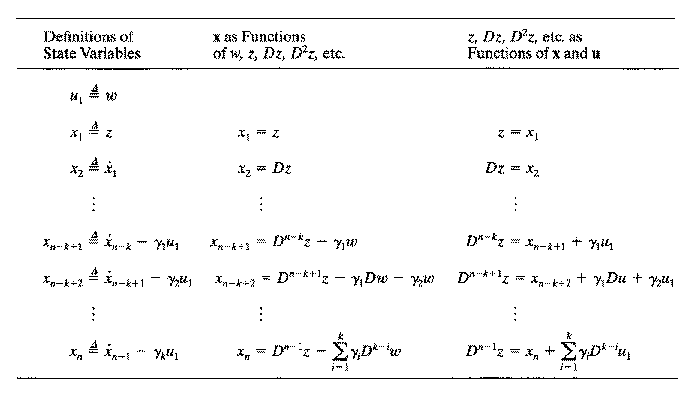微分流形的概念

微分流形的概念

参见条目：流形

具体说来,设M是一个豪斯多夫拓扑空间。U是M的开集,h是U到n维欧氏空间R的开集(常取为单位球内部或立方体内部等等)上的一个同胚映射,则(U，h)称为一个坐标图,U称为其中点的一个坐标邻域。设M为开集系{Uα}所覆盖,则(Uα,hα)的集合称为M的一个坐标图册。如果M的坐标图册中任何两个坐标图都是C相关的,则称M有C微分结构,又称M为n维的C微分流形。C相关是指流形M上同一点的不同坐标之间的变换关系是C可微分的(k=0,1,…,∞或ω)，依通常记号C表示解析函数。具体来说, 如p∈Uα∩Uβ,(x,）(x)(i=1,…,n)分别是p在两个坐标图(Uα,hα)，(Uβ,hβ)下的(局部)坐标,即那么它们之间的关系式可表为而ƒ关于x（j=1,2，…，n）具有直到k次的连续导数。k=0时,M是拓扑流形；k>0时,就是微分流形；k=ω时，是解析流形。C流形又常称为光滑流形。如果微分流形M是一个仿紧或紧致拓扑空间，则称M为仿紧或紧致微分流形。如果可选取坐标图册使微分流形M中各个坐标邻域之间的坐标变换的雅可比行列式都大于零，则称这个流形是可定向的。球面是可定向的，麦比乌斯带是不可定向的。

同一拓扑流形可以具有本质上不同的微分结构。米尔诺（John Milnor）首先发现作为一个拓扑流形，七维球面上可有不同于标准微分结构的怪异微分结构。后来弗里德曼（Michael Freedman）等得出如下的重要结果:四维欧氏空间中也有多种微分结构，这与其他维数的欧氏空间只有惟一的微分结构有着重大区别。